Factorización. Los 10 Casos de Factorización (con ejemplos) + ejercicios de factoreo resueltos. Si tienes alguna inquietud recuerda contactarnos a través de nuestras redes sociales, o regístrate y déjanos un comentario en esta página. También puedes participar en el WhatsApp. Si usas Telegram  ingresa al siguiente enlace.

En matemáticas, los 10 casos de factorización (o factoreo), son aquellos que buscan simplificar el estudio de los polinomios, haciendo uso de reglas nemotecnicas que predicen resultados de casos muy comunes, entre los cuales tenemos:

• Factor común.
• Factor común por agrupación de términos.
• Trinomio cuadrado perfecto.
• Diferencia de cuadrados.
• Trinomio cuadrado perfecto por adición o sustracción.
• Trinomio de la forma X^2 + BX + C
• Suma o diferencia de potencias.
• Trinomio de la forma aX^2 + bX + c.
• Suma y diferencia de cubos.
• Raíces de un polinomio.

VIDEO: Interpretación de los 10 Casos de Factorizacion

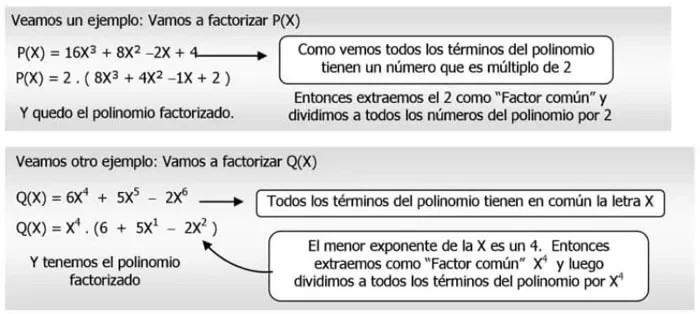
Caso #1 – Factoreo por factor común

Cuando en los diversos términos de un polinomio participa un mismo factor, se dice que se le saca como factor común, para lo cual, se escribe e inmediatamente, después, dentro de un paréntesis se anotan los cocientes que resulten de dividir cada uno de los términos del polinomio entre el factor común.

Por ejemplo

Otros ejemplos: a) 8X + 2Y = 2 * (4X + Y) (En este caso el factor común es 2)
b) a2 + 2a = a(a+2)

c) 10b + 30ab2 = 10b(1 + 3ab)

d) 10a2 + 5a + 15a3 = 5a(2a + 1 + 3a2)

e) 5a3b2x + 15a4bx2 − 35a2b2x4y5 = 5a2bx(ab + 3a2x − 7bx3y5 )

Caso #2 – Factoreo por agrupamiento

Algunas veces en un polinomio los términos no contienen ningún factor común, pero pueden ser separados en grupos de términos con factor común.

Este método consiste en formar grupos, los más adecuados, para factorizar cada uno como más convenga en cada caso y lograr finalmente la factorización total de la expresión.

Ejemplos: Factorizar:

a) 5a + 5b + ax + bx . Agrupando los términos que tengan algún factor común se tiene: 5(a+b)+ x(a+ b) = (a +b)(5 + x) o también a(5+ x)+ b(5+ x) = (a +b)(5 + x)

b) x2 +ax+bx+ab= x(x+a)+b(x+a)=(x+a)(x+b)

c) 8ax−bx+8ay−by) =8a(x+y)−b(x+y)=(x+y)(8a −b)

Caso #3 – Factoreo por Trinomio cuadrado perfecto.

En este caso se tiene un polinomio de grado dos y cuyas raíces están en el campo de los números reales, por ejemplo.

X^2 ± 2*a*X + a^2 = (X ± a)^2

Caso #4 – Factoreo por diferencia de cuadrados.

Este es el caso de un producto de dos binomios cuya diferencia es solo el signo del segundo término.

(a + b) * (a – b) = a^2 – b^2

Caso #5 – Factoreo por Trinomio cuadrado perfecto por adición o sustracción.

Este caso ocurre cuando se posee un trinomio cuadrado perfecto en el que no es posible obtener dos raíces iguales y en el campo de los números reales. Se suma y resta la cantidad necesaria para obtener la forma del trinomio deseado.

X^2 + 2X – 5 = (X^2 + 2X + 2) – 2 – 5 = (X + 1)^2 – 7

Caso #6 – Factoreo por Trinomio de la forma X^2 + BX + C

En este caso de factorización se tiene un trinomio que tiene raíces reales pero que no son ni repetidas ni siguen el del caso anterior. Para ello se deben conseguir las raíces del polinomio.

X^2 – 5X + 6 = (x – 3) * (x + 2)

Caso #7 – Factoreo por Suma o diferencia de potencias.

Se trata de descomponer factores que compartan una misma potencia.

X^3 + 27 = X^3 + 3^3 = (X + 3) * (X^2 – 3X + 9)

Caso #8 – Factoreo por trinomio de la forma aX^2 + bX + c.

Para este caso se puede factorizar utilizando la ecuación de la resolvente la cual es la siguiente:

X = – b ± √b^2 – 4*a*c / 2*a

4X^2 + 12X + 9

X = – 12 ± √(12)^2 – 4*4*9 / 2*4

X1 = X2 = -1,5

4X^2 + 12X + 9 = (X + 1,5) * (X + 1,5)

Caso #9 – Factoreo por Suma y diferencia de cubos.

Son de la siguiente forma:

a^3 ± b^3 = (a ± b) * (a^2 ± a*b + b^2)

Caso #10 – Factoreo por raíces de un polinomio.

Ejercicios de factoreo resueltos:

Factorización de Polinomios: